3D visualization of Sutherland-Hodgman algorithm (polygon clipping)
Τρισδιάστατη οπτικοποίηση του αλγορίθμου Sutherland-Hodgman (αποκοπή πολυγώνων)
IntroductionΕισαγωγή
The Sutherland-Hodgman algorithm is an algorithm for clipping polygons. Clipping is the process of determining what region of space is within another region of space. It's a very important algorithm with applications in computer graphics (e.g. intersections calculation, rendering decisions), physics simulations (e.g. collision detections) and in many other fields. It works by extending each line of the convex clip polygon in turn and selecting only vertices from the subject polygon that are on the visible side. The Sutherland–Hodgman algorithm can also be extended into the 3D space by clipping the polygon paths based on the boundaries of planes (defined for example by other polygons/polyhedra or by the viewing space).
Ο αλγόριθμος Sutherland-Hodgman είναι ένας αλγόριθμος για αποκοπή πολυγώνων. Αποκοπή ονομάζουμε τη διαδικασία του καθορισμού ποιά περιοχή ενός χώρου βρίσκεται σε επικάλυψη με μια άλλη περιοχή του χώρου. Πρόκειται για έναν πολύ σημαντικό αλγόριθμο με εφαρμογές στα γραφικά υπολογιστών (π.χ. υπολογισμός τομών, καθορισμός απεικoνίσεων), προσομοιώσεις φυσικής (π.χ. ανίχνευση συγκρούσεων) και σε πολλά άλλα πεδία. Λειτουργεί, εκτείνοντας κάθε φορά μια γραμή του κυρτού πολυγώνου αποκοπής και επιλέγοντας μόνο τις κορυφές από το υποκείμενο πολύγωνο που βρίσκονται στην ορατή πλευρά. Ο αλγόριθμος Sutherland-Hodgman μπορεί να επεκταθεί και στον τρισδιάστατο χώρο, αποκόπτωντας τις διαδρομές των πολυγώνων με βάση τα όρια από επίπεδα (που ορίζονται για παράδειγμα από άλλα πολύγωνα/πολύεδρα ή από το χώρο θέασης).

Geometric ClassesΓεωμετρικές Κλάσεις
Class PointΚλάση Point
First of all, we need a (3D) "Point" class:
Πρώτα από όλα, χρειαζόμαστε μια κλάση "Point" (3Δ):
class Point {
private:
double_t _x, _y, _z;
public:
Point(double_t x = 0, double_t y = 0, double_t z = 0) : _x(x), _y(y), _z(z) {}
void setX(double_t x) { _x = x; };
void setY(double_t y) { _y = y; };
void setZ(double_t z) { _z = z; };
double_t getX() const { return _x; }
double_t getY() const { return _y; }
double_t getZ() const { return _z; }
double_t length() const { return sqrt(_x * _x + _y * _y + _z * _z); };
double_t dot (Point q) const { return _x * q._x + _y * q._y + _z * q._z; };
Point cross (Point q) const { return Point(_y * q._z - _z * q._y, _z * q._x -
_x * q._z, _x * q._y - _y *q._x); }
Point normalized() const { float l=length(); return Point(_x/l,_y/l,_z/l); }
Point operator+(Point v) const { return Point(_x + v.getX(), _y + v.getY(),
_z + v.getZ()); }
Point operator-(Point v) const { return Point(_x - v.getX(), _y - v.getY(),
_z - v.getZ()); }
Point operator*(double_t f) const { return Point(_x * f, _y * f, _z * f); }
friend ostream& operator<< (ostream& out, const Point& p)
{ return out << fixed << setprecision(6) << "("
<< p._x << ", " << p._y << ", " << p._z << ")"; }
};Class PolygonΚλάση Polygon
Next, we need a "Polygon" class:
Έπειτα, χρειαζόμαστε μια κλάση "Polygon":
class Polygon {
private:
vector<Point> _vertices; //Last vertex = First vertex.
public:
Polygon() {}
Polygon(vector<Point> vertices):
_vertices(vertices) { _vertices.push_back(_vertices[0]); }
void add(Point p) {
//Add a new vertex to the polygon. Last vertex = First vertex.
if (!_vertices.empty()) { _vertices.pop_back(); }
_vertices.push_back(p);
_vertices.push_back(_vertices[0]); }
vector<Point> getVertices() const { return _vertices; }
bool isEmpty() const { return _vertices.empty(); }
void drawGL(float r, float g, float b) const {
unsigned int n = _vertices.size();
glBegin(GL_POLYGON);
for (unsigned int i=0; i < n; i++) {
glColor3f(r/(i+0.1), g/(i+0.1), b/(i+0.1));
glVertex3f(_vertices[i].getX(), _vertices[i].getY(), _vertices[i].getZ());
}
glEnd();
}
void printCoordsGL() const {
for (unsigned int i=0; i < _vertices.size(); i++) {
glRasterPos3f(_vertices[i].getX(), _vertices[i].getY(), _vertices[i].getZ());
stringstream stream;
stream << fixed << setprecision(1) << "(" << _vertices[i].getX() << ","
<< _vertices[i].getY() << "," << _vertices[i].getZ() << ")";
string s = stream.str();
for (unsigned int j = 0; j < s.length(); j++)
{ glutBitmapCharacter(GLUT_BITMAP_TIMES_ROMAN_10, s[j]); }
}
}
friend ostream& operator<< (ostream& out, const Polygon& p) {
if (p._vertices.empty()) { return out << "empty" << endl; }
for (unsigned int i=0; i < p._vertices.size()-1; i++)
{ out << p._vertices[i] << endl; }
return out; }
};Class PlaneΚλάση Plane
In geometry, a plane is a flat surface that extends forever in two dimensions (it has no thickness). In essence, that means a plane is the two-dimensional analogue of a point (zero dimensions) or a line (one dimension). Here is our "Plane" class:
Στη γεωμετρία, ένα επίπεδο είναι μια επιφάνεια που εκτείνεται σε δύο διαστάσεις στο άπειρο (δεν έχει πάχος). Στην ουσία, αυτό σημαίνει ότι ένα επίπεδο είναι το διδιάστατο ανάλογο ενός σημείου (μηδέν διαστάσεις) ή μιας γραμμής (μία διάσταση). Εδώ έχουμε, λοιπόν, μια κλάση "Plane":
class Plane {
private:
Point _normal, _v1, _v2, _v3;
double_t _d;
public:
Plane(Point normal, double_t d): _normal(normal), _d(d) {}
Plane(Point v1, Point v2, Point v3): _v1(v1), _v2(v2), _v3(v3) {
//Create a plane from 3 non-colinear points (i.e. triangle)
_normal = (v2 - v1).cross(v3 - v1).normalized();
_d = -_normal.dot(v1); }
Point intersectionPoint(Point p1, Point p2) const {
//Return the intersection point of a line passing two points and this plane
return p1 + (p2 - p1) * (-distance(p1) / _normal.dot(p2 - p1)); };
void invert() { _normal = _normal * (-1); }
Point getNormal() const { return _normal; }
Polygon getTriangle() const { vector<Point> points = {_v1, _v2, _v3};
return Polygon(points); }
double_t distance(Point q) const { return _normal.dot(q) + _d; }
};Class PyramidΚλάση Pyramid
Last, for our clipping polyhedron, let's create a "Pyramid" class:
Τέλος, για το πολύεδρο αποκοπής μας, ας δημιουργήσουμε μια κλάση "Pyramid":
class Pyramid {
private:
Point _apex;
vector<Point> _vertices;
public:
Pyramid() {}
Pyramid(Point apex, vector<Point> vertices):
_apex(apex), _vertices(vertices) { _vertices.push_back(_vertices[0]); }
void setApex(Point apex) { _apex = apex; }
void addBasepoint(Point apex) {
//Add a new vertex to the polygon. Last vertex = First vertex.
if (!_vertices.empty()) { _vertices.pop_back(); }
_vertices.push_back(apex);
_vertices.push_back(_vertices[0]);
}
Point centroid() const {
unsigned int n = _vertices.size();
Point centroid = _apex;
for (unsigned int i = 0; i < n; i++) { centroid = centroid + _vertices[i]; }
centroid = centroid * (1.0 / (n + 1));
return centroid;
}
vector<Plane> faces2planes() const {
vector<Plane> planes;
int n = _vertices.size();
Point pyr_centroid = centroid();
planes.reserve(n + 1);
for (int i = 0; i < n - 1; i++) {
Plane pl = Plane(_apex, _vertices[i], _vertices[i+1]);
if (pl.distance(pyr_centroid) > 0) { pl.invert(); }
planes.push_back(pl);
}
//Add a plane for the base of the pyramid
Plane pl = Plane(_vertices[2], _vertices[1], _vertices[0]);
if (pl.distance(pyr_centroid) > 0) { pl.invert(); }
planes.push_back(pl);
return planes;
}
void drawGL(float r, float g, float b) const {
for (unsigned int i = 0; i < _vertices.size() - 1; i++) {
glBegin(GL_TRIANGLES);
glColor3f(r/0.1, g/0.1, b/0.1);
glVertex3f(_apex.getX(), _apex.getY(), _apex.getZ());
glColor3f(r/1.1, g/1.1, b/1.1);
glVertex3f(_vertices[i].getX(), _vertices[i].getY(), _vertices[i].getZ());
glColor3f(r/2.1, g/2.1, b/2.1);
glVertex3f(_vertices[i+1].getX(), _vertices[i+1].getY(), _vertices[i+1].getZ());
glEnd();
}
}
void printCoordsGL() const {
glRasterPos3f(_apex.getX(), _apex.getY(), _apex.getZ());
stringstream stream_apex;
stream_apex << fixed << setprecision(1) << "(" << _apex.getX() << ","
<< _apex.getY() << "," << _apex.getZ() << ")";
string str_apex = stream_apex.str();
for (unsigned int i = 0; i < str_apex.length(); i++)
{ glutBitmapCharacter(GLUT_BITMAP_TIMES_ROMAN_10, str_apex[i]); }
for (unsigned int i = 0; i < _vertices.size(); i++) {
glRasterPos3f(_vertices[i].getX(), _vertices[i].getY(), _vertices[i].getZ());
stringstream stream;
stream << fixed << setprecision(1) << "(" << _vertices[i].getX() << ","
<< _vertices[i].getY() << "," << _vertices[i].getZ() << ")";
string s = stream.str();
for (unsigned int j = 0; j < s.length(); j++)
{ glutBitmapCharacter(GLUT_BITMAP_TIMES_ROMAN_10, s[j]); }
}
}
};Sutherland-Hodgman
ImplementationΥλοποίηση
Here is our implementation of the Sutherland-Hodgman algorithm in three dimensions:
Εδώ είναι η υλοποίησή μας για τον αλγόριθμο Sutherland-Hodgman στις τρεις διαστάσεις:
Polygon SutherlandHodgman(const Polygon startingPolygon, vector<Plane> clippingPlanes) {
double_t D1, D2 = 0;
Polygon polygon = Polygon(startingPolygon);
for (unsigned int c = 0; c < clippingPlanes.size(); c++) {
if (polygon.isEmpty()) { return polygon; }
Polygon clippedPolygon = Polygon();
vector<Point> points = polygon.getVertices();
for (unsigned int i = 0; i < points.size() - 1; i++) {
D1 = clippingPlanes[c].distance(points[i]);
D2 = clippingPlanes[c].distance(points[i+1]);
if ((D1 <= 0) && (D2 <= 0))
{ clippedPolygon.add(points[i+1]); }
else if ((D1 > 0) && ((D2 > -EPSILON) && (D2 < EPSILON)))
{ clippedPolygon.add(points[i+1]); }
else if (((D1 > -EPSILON) && (D1 < EPSILON)) && (D2 > 0))
{ continue; }
else if ((D1 <= 0) && (D2 > 0))
{ clippedPolygon.add(clippingPlanes[c].intersectionPoint(points[i],
points[i+1])); }
else if ((D1 > 0) && (D2 <= 0))
{ clippedPolygon.add(clippingPlanes[c].intersectionPoint(points[i],
points[i+1]));
clippedPolygon.add(points[i+1]); }
}
polygon = Polygon(clippedPolygon); // keep on working with the new polygon
}
return polygon;
}Step-by-step visualizationΟπτικοποίηση βήμα προς βήμα
Ιn my opinion, the best way to understand an algorithm is to dissect it and visualize it, one step at a time. Therefore, we created the stepSutherlandHodgman function (a modified version of our previous implementation), which proceeds in steps.
Κάτα τη γνώμη μου, ο καλύτερος τρόπος για να κατανοήσουμε έναν αλγόριθμο είναι να τον αναλύσουμε και να τον οπτικοποιήσουμε βήμα προς βήμα. Για αυτό, φτιάξαμε τη συνάρτηση stepSutherlandHodgman (μια τροποποιημένη εκδοχή της προηγούμενης υλοποιήσης μας), η οποία προχωράει σε βήματα.
For the visualization, we used GLUT (OpenGL Utility Toolkit), a window system independent toolkit for writing OpenGL programs. It implements a simple portable API for OpenGL, so we can write a single OpenGL program that works on both Windows and X11 systems. The function glutDisplayFunc sets the display callback for the current window (it is called when GLUT determines that the normal plane for the window needs to be redisplayed). The glutIdleFunc sets the idle callback (so a GLUT program can perform background tasks).
Για την οπτικοποίηση, χρησιμοποιήσαμε το GLUT (OpenGL Utility Toolkit), μια εργαλειοθήκη για να γράφουμε OpenGL προγράμματα, ανεξάρτητα από το γραφικό σύστημα παραθύρων. Υλοποιεί μια απλή, φορητή Διεπαφή Προγραμματισμού Εφαρμογών (Application Programming Interface, API) για το OpenGL, ώστε να μπορούνε να γράψουμε ένα και μοναδικό πρόγραμμα που δουλεύει, τόσο στα Windows, όσο και στα X11 συστήματα. Η συνάρτηση glutDisplayFunc ορίζει τη συνάρτηση επανάκλησης για την απεικόνιση στο τρέχον παράθυρο (καλείτε όταν το GLUT κρίνει ότι χρειάζεται να ανανεωθεί η απεικόνιση). Η συνάρτηση glutIdleFunc ορίζει τη συνάρτηση επανάκλησης για την αδράνεια (ώστε ένα πρόγραμμα GLUT να μπορεί να επιτελεί διεργασίες στο παρασκήνιο).
For mouse interaction, we used GLT ZPR, a mouse manipulation module for C or C++ GLUT/OpenGL programs. With the addition of two lines of code, any GLUT based OpenGL program can include mouse-based rotation (left click), zooming (middle click), and panning(right click). Moreover, the middle button can be emulated by using both left and right together. This module works by supplying GLUT callback functions for glutReshapeFunc, glutMouseFunc and glutMotionFunc which manage the OpenGL modelview matrix, according to mouse events received via GLUT.
Για την αλληλεπίδραση με το ποντίκι, χρησιμοποιήσαμε το GLT ZPR, που επιτρέπει τον χειρισμό του ποντικιού σε προγράμματα GLUT/OpenGL (γραμμένα σε C ή C++). Με την προσθήκη δύο γραμμών κώδικα, οποιοδήποτε πρόγραμμα OpenGL βασισμένο στο GLUT μπορεί να περιλαμβάνει χειρισμούς με το ποντικί οπως περιστροφή (αριστερό κουμπι), μεταβολή της εστιακής απόστασης (μεσαίο κουμπι) και μετατόπιση (δεξί κουμπί). Επιπλέον, το μεσαίο κουμπί μπορεί να προσομοιωθεί πατώντας το αριστερό και το δεξί κουμπί ταυτόχρονα. Το ZPR λειτουργεί παρέχοντας συναρτήσεις επανάκλησης για τις glutReshapeFunc, glutMouseFunc και glutMotionFunc που διαχειρίζονται τον πίνακα μετασχηματισμού Μοντέλου-Κάμερας (modelview) του OpenGL, σύμφωνα με τα ερεθίσματα που λαμβάνονται από το ποντίκι μέσω του GLUT.
Last, in order to proceed to the next step of the algorithm, just press any key in the keyboard (except "Esc" which is to quit the app).
Τέλος, για να προχωρήσετε στο επόμενο βήμα του αλγόριθμου, απλα πατήστε ένα οποιοδήποτε πλήκτρο στο πληκτρολόγιο (εκτός από το "Esc" που είναι για την έξοδο από την εφαρμογή).
/* GLOBAL VARIABLES */
Polygon POL;
Pyramid PYR;
vector<Polygon> FACES;
unsigned int COUNTER = 0;
bool CONTINUE = false;
Polygon stepSutherlandHodgman(const Polygon inputPolygon, Plane clippingPlane) {
double_t D1, D2 = 0;
Polygon polygon = Polygon(inputPolygon);
if (polygon.isEmpty()) { return polygon; }
Polygon clippedPolygon = Polygon();
vector<Point> points = polygon.getVertices();
for (unsigned int i = 0; i < points.size() - 1; i++) {
D1 = clippingPlane.distance(points[i]);
D2 = clippingPlane.distance(points[i+1]);
if ((D1 <= 0) && (D2 <= 0))
{ clippedPolygon.add(points[i+1]); }
else if ((D1 > 0) && ((D2 > - EPSILON) && (D2 < EPSILON)))
{ clippedPolygon.add(points[i+1]); }
else if (((D1 > - EPSILON) && (D1 < EPSILON)) && (D2 > 0))
{ continue; }
else if ((D1 <= 0) && (D2 > 0))
{ clippedPolygon.add(clippingPlane.intersectionPoint(points[i],
points[i+1])); }
else if ((D1 > 0) && (D2 <= 0))
{ clippedPolygon.add(clippingPlane.intersectionPoint(points[i],
points[i+1]));
clippedPolygon.add(points[i+1]); }
}
FACES.push_back(clippingPlane.getTriangle());
POL = clippedPolygon;
glutPostRedisplay();
return clippedPolygon;
}
void normalKeyDownGL(unsigned char Key, int x, int y) {
switch(Key){
case 27: exit(1); break; //Press "Escape" for exit
default: CONTINUE = true; //Press any key to continue
}
}
void displayGL() {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
POL.drawGL(0.1f, 1.0f, 0.0f);
glColor3f(1.0f, 1.0f, 1.0f);
POL.printCoordsGL();
if (COUNTER == 0) {
PYR.drawGL(1.0f, 0.0f, 0.0f);
glColor3f(1.0f, 1.0f, 1.0f);
PYR.printCoordsGL();
} else {
for (unsigned int j = 0; j < FACES.size(); j++) {
FACES[j].drawGL(1.0f, 0.0f, 0.0f);
glColor3f(1.0f, 1.0f, 1.0f);
FACES[j].printCoordsGL();
}
}
glutSwapBuffers();
}
void idleGL(void) {
if (CONTINUE && COUNTER < PYR.faces2planes().size()) {
Polygon clipped = stepSutherlandHodgman(POL, PYR.faces2planes()[COUNTER]);
vector<Point> points = clipped.getVertices();
for (unsigned int i = 0; i < points.size() - 1; i++) { cout << points[i] << endl; }
cout << endl;
CONTINUE = false;
COUNTER++;
}
}
int main(int argc, char** argv)
{
Point pyramid_apex = Point(0,0,2);
vector<Point> pyramid_vertices { Point(-1, -1, 0), Point(+1, -1, 0),
Point(+1, +1, 0), Point(-1, +1, 0)};
//vector<Point> triangle_vertices {Point(-2, -5, 1), Point(0, 0, 1), Point(-2, +5, 1)};
vector<Point> triangle_vertices { Point(0, 0, 2), Point(2, -5, 1),
Point(0, 0, 0), Point(-2, +5, 1)};
Pyramid pyramid(pyramid_apex, pyramid_vertices);
Polygon triangle(triangle_vertices);
cout << "RESULT" << endl << SutherlandHodgman(triangle, pyramid.faces2planes());
POL = triangle;
PYR = pyramid;
//GLUT initialization
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA | GLUT_DEPTH);
glutInitWindowSize(600, 600);
glutInitWindowPosition(25, 25);
glutCreateWindow("Test");
glScalef(0.25,0.25, 0.25);
//Configure GLUT callback functions
glutDisplayFunc(displayGL);
glutIdleFunc(idleGL);
glutKeyboardFunc(normalKeyDownGL);
//Configure ZPR module
zprInit();
//Enable GL settings
glEnable(GL_DEPTH_TEST);
//Enter GLUT event loop
glutMainLoop();
return 0;
}ScreenshotsΣτιγμιότυπα
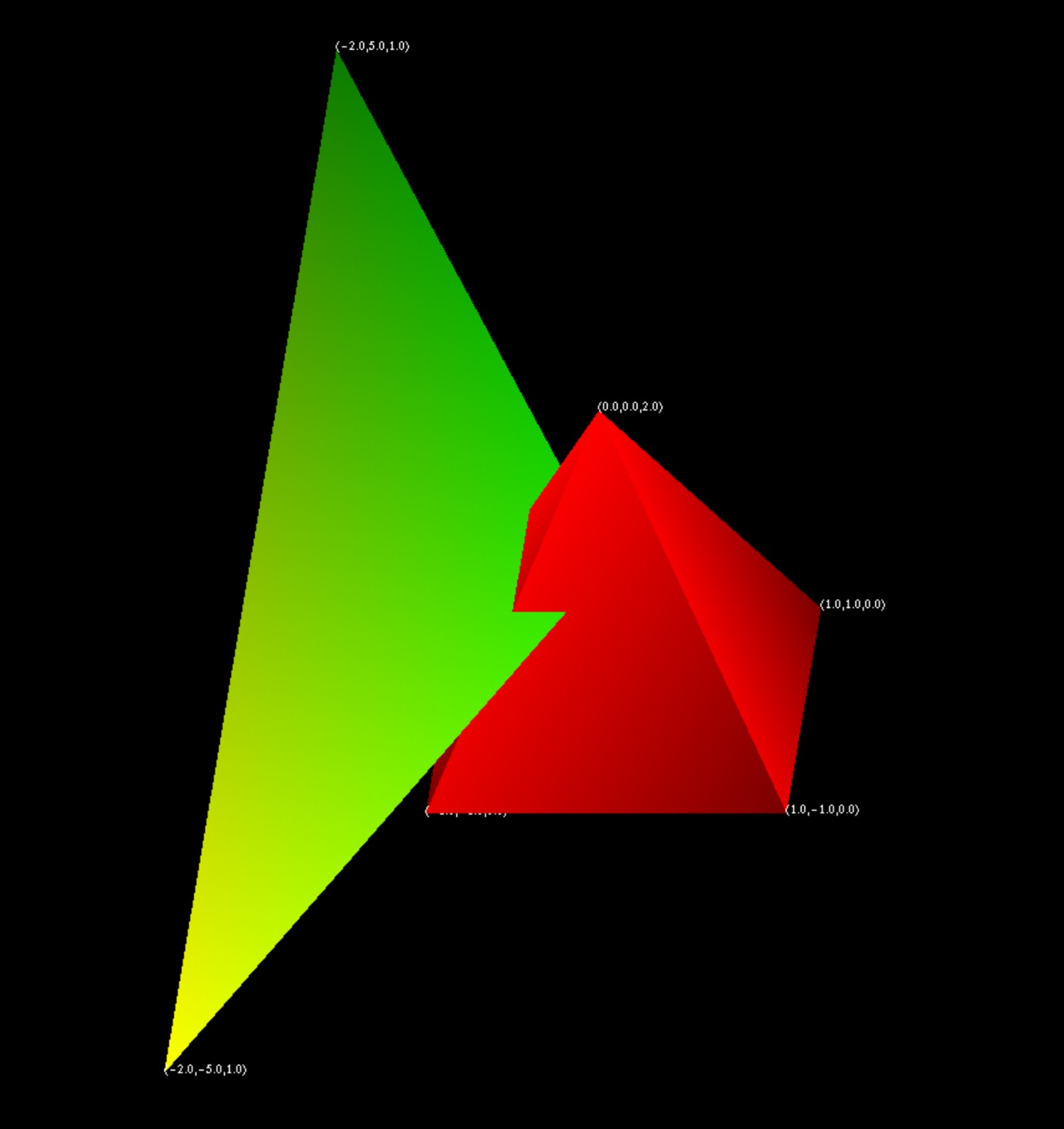
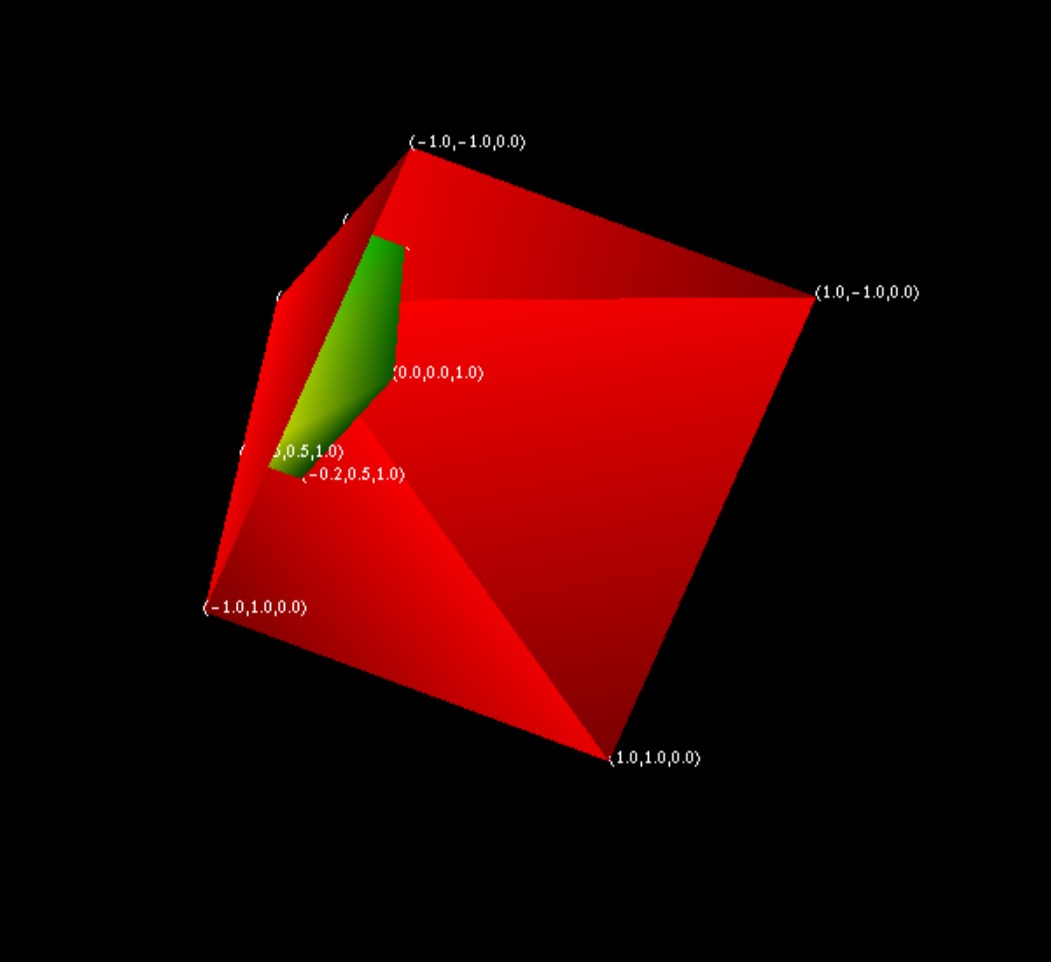
Full source code and executable binariesΠλήρης κώδικας και εκτελέσιμα
You can download the full source code and the executable binaries (for Linux and Windows) from here.
Μπορείτε να κατεβάσετε τον πλήρη πηγαίο κώδικα και τα εκτελέσιμα αρχεία (για Linux και Windows) από εδώ.